理解堆与堆排序

2017-04-27

|已阅： 1

一、堆的概念

一般常说的堆是一个完全二叉树
并且任意节点的值都大于（或小于）子节点

大于子节点的是最大堆
小于子节点的是最小堆

二、堆的表示方式

堆是长这个样子的（最大堆）：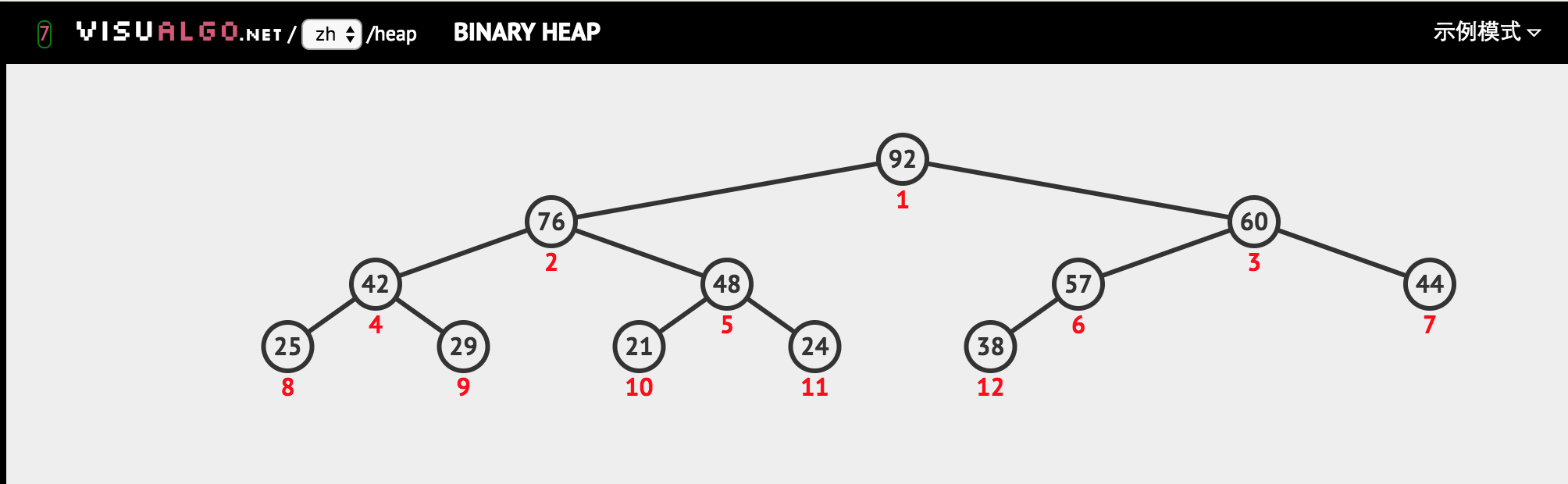

在程序中使用数组表示，从上到下，一行一行的放入数组中。也就是：

1	{92,76,60,42,48,57,44,25,29,21,24,38}

三、堆排序

理解了堆的基本概念我们再来看一下堆排序。

基本原理

从堆的特点可以看出，根节点就是当前给出的数据中最大/最小的。所以（以最大堆排序为例）：

把数组的第0个取出
再把最后一个放到第0位
因为最后一个不一定是剩余数据中最大的
所以调整堆
重复1-4步直到剩最后一个

这么说有点干巴，可以去看一下动画演示就明白了二叉堆

实现

先上代码：

import java.util.Arrays;
/**
 * Created by ixx on 2017/4/26.
 */
public class T {
    public static void main(String args[]){
        int[] t = {2,7,26,25,19,17,1,90,3,36,66,3,9,88};
        //创建堆
        t = createMaxHeap(t);
        for(int i : t){
            System.out.print(i+",");
        }
        System.out.println("");

        //堆排序
        while(t.length > 1){
            System.out.print(t[0] + ",");
            t[0] = t[t.length-1];
            t = createMaxHeap(Arrays.copyOfRange(t, 0, t.length-1));
        }
        System.out.print(t[0] + ",");
    }
    //创建(调整)堆
    public static int[] createMaxHeap(int[] t){
        for(int i = 1; i< t.length; i++){
            for (int n=i, m = i/2 + 1; n>0; n=n-m, m = n/2+1) {
                if (t[n] > t[n-m]) {//如果当前节点大于父节点,则交换数据,并循环判断是否大于父节点的父节点...
                    int tmp = t[n];
                    t[n] = t[n-m];
                    t[n-m] = tmp;
                } else { //否则跳出当前循环,判断下一个元素
                    break;
                }
            }
        }
        return t;
    }
}

这里最不好理解的应该是这句：

1 2	for (int n=i, m = i/2 + 1; n>0; n=n-m, m = n/2+1) { ...

解释一下n和m的意义

n是指向当前元素的下标，如果当前元素大于父节点发生了交换，n依然指向当前元素
m是n指向元素与父节点在数组中的下标差值，即n-m为父节点下标

为什么m = n/2+1?
让我们回过头来看一下堆转换后的数组：

________数据：92,76,60,42,48,57,44,25,29,21,24,38
________下标： 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11
_与父节点差值： 0, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6

比如最后一个38，它的下标是11,差值是6,所以父节点就是11-6=5，也就是57，对应图看一下，没有问题
那么找一下这个差值和规律你就能发现差值=下标/2+1

执行结果

90,66,88,25,36,9,17,2,3,19,26,3,7,1,
90,88,66,36,26,25,19,17,9,7,3,3,2,1,

四、优化

上边的代码简单实现了堆排序，但是只有首次创建堆我们需要使用createMaxHeap方法进行全遍历
进行堆排序第4步的操作调整堆时，除了根节点，下边各子节点都已经是一个堆结构了，所以我们只需要将根节点按规则“下沉”就可以了，即：

找出子节点中最大的一个
判断是否大于当前节点
大于则交换并继续下沉，小于则结束

添加调整堆方法：

     /**
     * 调整堆
     * t 堆转换后的数组
     * i 当前下标
     */
    public  static void fixMaxHeap(int[] t,int i){
        int n = i*2+1;//左子节点下标
        if(n < t.length){
            //如果有右子节点且右子节点大于左子节点（取出最大的子节点下标）
            if(n+1 < t.length && t[n+1] > t[n]){
                n += 1;
            }
            if(t[n] > t[i]){//判断当前节点是否小于子节点,小于则交换并继续递归
                int tmp = t[i];
                t[i] = t[n];
                t[n] = tmp;
                fixMaxHeap(t, n);
            }
        }
    }

取子节点算下标大家对照之前的方法算一下就能得到。
再修改一下上边的堆排序代码：

        //堆排序
        while(t.length > 1){
            System.out.print(t[0] + ",");
            t[0] = t[t.length-1];
            t = Arrays.copyOfRange(t, 0, t.length-1);
            fixMaxHeap(t, 0);
        }

五、问题

为什么是最后一个？

按照堆的定义我们知道，最大的值是根节点，其次是它的两个子节点中的一个，去除根节点后为什么不拿最大的一个放到根节点上？
我们试一下

根节点移除
取它的子节点中最大的一个变更为根节点
变更后原来的位置空缺从子节点选取补充
直到没有子节点结束

也就是说最后总有一个空缺，除非这个空缺是最后一个元素，否则这个树就不在是完全二叉树了，也就不符合堆的定义了。

不符合定义行不行？

不符合定义就不能算是堆了，也就不算堆排序了，但也可以实现排序。只要是找一个合适的占位符去把空出来的数组下标补上并不影响正常的排序就可以了，这个下次实现一下试试。

六、说明:

文中的代码是我按自己的理解去实现的堆排序，如果有理解不到位的地方欢迎指正

本文作者： ixx
本文链接： http://blog.jisuye.com/2017/04/27/heap_and_heap_sort/
版权声明： 本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。转载请注明出处！